Our recent unit in Geometry has focused on Food Apartheid. This week, we began with a very sparse prompt asking students where a new grocery store should be built in relation to two existing neighborhoods (activity linked here):
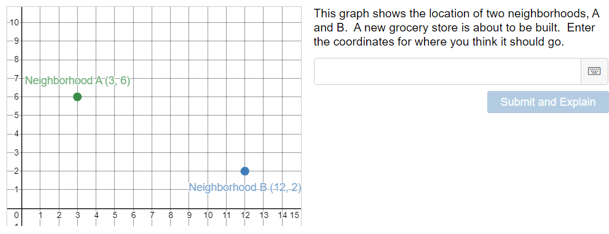
After entering their location and explanation, students were asked to add a sketch to illustrate the thinking behind their decision. Next week, we will share and compare thinking. Perhaps not surprisingly most students attempted to locate the grocery store directly in the middle of the invisible line connecting the two neighborhoods.
Though we have not discussed ‘midpoint’ in class, it is of course the mathematical content that generated the idea for this activity. Yet I am also reminded of this quote from Tayari Jones’s 2018 article in Time:
The middle is a point equidistant from two poles. That’s it. There is nothing inherently virtuous about being neither here nor there. Buried in this is a false equivalency of ideas, what you might call the “good people on both sides” phenomenon. When we revisit our shameful past, ask yourself, Where was the middle? Rather than chattel slavery, perhaps we could agree on a nice program of indentured servitude? Instead of subjecting Japanese-American citizens to indefinite detention during WW II, what if we had agreed to give them actual sentences and perhaps provided a receipt for them to reclaim their things when they were released? What is halfway between moral and immoral?
Tayari Jones, Time 2018
If as Jones later writes, “justice seldom dwells in the middle”, then I feel compelled to examine what role this mathematical content plays elevating the importance of the middle. Without an intentional eye toward criticality, there is a risk of perpetuating harmful values and assumptions about nature of both mathematics and morality. In this specific case, the assumption that ‘the middle’ has inherent value.
Despite the open-ended nature of the task, nearly all students picked a location for the grocery store that was equidistant from the two neighborhoods (not all students, however – see Tangent 1). None asked for additional information about the neighborhoods like vehicle access, population, average age, average income, location to other grocery stores, etc. Of course, they were not prompted to, and they maybe are accustomed to intuiting the ‘right’ answer in an abstracted math problem.
Yet, I believe a central aim of education must be to develop a criticality in students so that they will instinctively and adamantly raise questions of context, challenge assumptions, and resist harmful abstraction. In hopes of pursuing a deeper criticality I am planning to open class next week with this prompt (linked here):
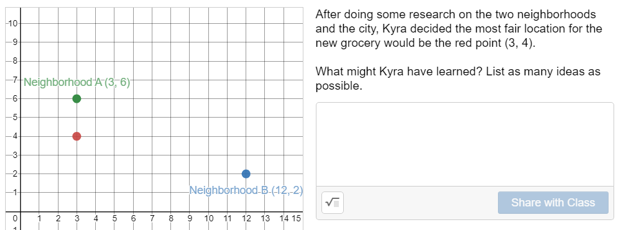
Of course, this task immediately widens the scope of inquiry beyond a narrow focus on midpoint. To develop criticality, I think there must be an openness in our pedagogy. As such, I did not design these prompts to be used merely to apply previously acquired content. Nor am I intending to lead students to the discovery of one specific concept. I am trying to create a context where mathematics can unfold naturally, where it can lead to deeper questions and divergent thought. This seems not only more representative of the true nature of mathematics but also more apt to encourage criticality.
Certainly, some of the student sketches will led us to build the concept of midpoint. But other student thinking (see the Tangents below) will lead to other ideas and questions because that’s how math should work. It should be a little wild and rich and unpredictable. When mathematical knowledge is constructed too narrowly there is little space for critical and creative thought, and there is no space to evaluate the underlying values in the mathematics itself. Thus, it can easily perpetuate potentially harmful ideas like the inherent value of the middle.
‘The middle’ has been and is a force for maintaining white supremacy and patriarchy in our country. In a recent interview with Fresh Air, Heather McGhee describes, “the typical white moderate in the center that we have to sort of hew towards, it’s always trimmed the sails of policy ambition, right? We can’t get too far out of the center. And the center is defined as this sort of white center-right moderate.”
If midpoint is going to be elevated in math class, it is important to help students develop a criticality about whether ‘midpoint thinking’ generalizes to other contexts. At the moment, I’m mulling over a few ideas for this:
- Have students submit examples of specific disagreements/debates/controversies that they often think about. Encourage them to include both personal and political examples. Review and select a few that would be good for the following student task: construct a line with each endpoint as different ‘side’ of the argument. Then, in each scenario discuss whether the midpoint makes sense and whether it is fair and just.
- Explore where an historic figure would fall on a left/right/center spectrum. This could be a super interesting exploration with someone like MLK. Someone who modern popular culture often de-radicalizes in a whitewashed effort to make him appear centrist. How has ‘midpoint thinking’ given us an inaccurate view of Dr. King’s work? How does it prevent that work from moving forward? Students could even explore historical and present data in answering these questions.
- A class discussion on Tayari Jones full article could also be interesting. In the future, I see a great deal of interdisciplinary potential in this and the above bullet.
Certainty, I am not trying to assert that the middle is always bad or undesirable. In some situations, the most just outcome may be found in the center. My main hope is that these activities show that the construction of mathematical knowledge does not happen in a vacuum – it is both shaped by and shapes our way of understanding and moving in the world. The practice of math is never neutral. Even in attempting to rectify the reductivity of ‘midpoint thinking’ the activities I propose above frame disagreements as oppositional and mutually exclusive which is also not right for every context.
My hope is that activities like this will help students learn to evaluate the values and assumptions inherent in any mathematics. That they can see and interrogate the constant exchange between mathematics and systems of power. In other words, I am hoping they experience a math that does not ‘dwell in the middle’ so they can be a part of creating a math that strives for justice.
_________________
Reflection 1: I wanted to begin with a fairly open and context-less task because I thought it would provide more space for creative student thought. And I also just wanted to assess their natural reactions. I do wonder what would have been different if before asking them to place a point I asked, “what other information would you like to know before making your decision?” I often think of teaching as an act of holding things in tension. Sometimes it is important to offer a scaffold to criticality from the beginning. Sometimes we need to assess how students have developed in exercising criticality on their own. For the future, I am thinking about how to be more explicit about making such criticality a daily habit in my classroom.
Tangent 1: Some students’ sketches revealed they were thinking of total distance as the sum of horizontal and vertical distance, rather than the straight-line distance. In other words, distance as it would be measured on the roads and sidewalks one uses to get from the place to place. Such thinking could open discussions about the non-Euclidian, taxicab geometry. It also calls attention to another bias around how distance is conceived of in high school mathematics. The straight-line, Distance Formula distance conceptualized in high school mathematics is given more precedence than their taxicab conception of distance which actually more accurately models distance in many contexts.
Tangent 2: Several students chose a location for the grocery store that appeared equidistant to both neighborhoods but not directly in between them. Such thinking might lead us to ask how many other such points exist and then begin to explore the construction and properties of a perpendicular bisector.
Tangent 3: One student attempted to find the midpoint by drawing two congruent parallel lines and then using those as guides to find the ‘middle’. This could have potential for ‘constructing’ the midpoint by drawing the diagonals of the parallelogram.
Tangent 4: It could also be interesting to question the virtue of the midpoint within the domain of traditional mathematics itself. Are there more interesting areas of focus? The Koch Curve, for instance, is generated by splitting a segment into thirds rather than half. Some might argue that the midpoint formula is a necessary prerequisite for future mathematics like finding a Midpoint Riemann Sum in Calculus (though a student in Calculus would probably be able to grasp a quick introduction to the midpoint formula even if they had never seen it before). But even for Riemann Sums, it could be interesting to explore whether there are situations in which the midpoint method does not provide the best approximation of area.