What counts as ‘doing mathematics’? The math often and traditionally done in school offers one answer to that question. But, it is an answer that is far too narrow. In class, I’ve tried to help students explore a bigger answer to that question by examining some of the work of renowned music and style icon Beyoncé in the context of a unit on geometric transformations (reflections, rotations, and translations).
Music
Music maintains our interest by holding repetition and variation in tension. In the first minute and a half of Love on Top, Beyoncé establishes the chords and melody for the song. The shape of the notes can almost be heard. Then, keeping the shape the same (repetition) she shifts the pitch up a half step (variation), and then it happens again, and again…. It’s the sound of a translation (or in musical terms a transposition). It creates a compelling and impressive effect. It’s an effect also used by Dolly Parton in Here You Come Again, REM in Stand, and BTS in Dynamite.
Translations are also used as a fundamental element of music composition. The composer establishes a simple musical idea (or riff). That riff is then played again or translated forward in the measure – repetition. At certain points, the shape of the musical idea shifts up or down – variation. It’s new enough to grab our attention, but familiar enough not to jar it. The piano intro to the song Halo by Beyoncé provides a prefect example of this. Below is a simplified version of the sheet music and piano roll (the transitional fills at the end of each measure have been removed).

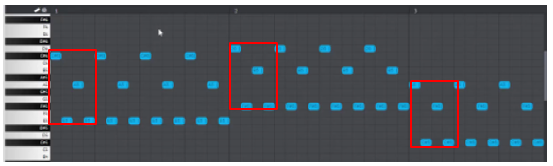
You may notice that in some cases the shape of the notes does not appear to perfectly maintained. This poses two interesting points of mathematical investigation. First, we could discuss how distance (and thus shape) is measured music: chromatically or by a note’s relative position in the chord or scale. And second, there’s ever present tension between a strict theoretical model and what works (or sounds good) in practice.
Some music, however, does use a more rigid translation structure. Led Zeppelin’s Heartbreaker is an excellent example. The 12-bar blues is the foundation of many songs in blues, jazz, and popular music, and it could be conceptualized through geometric translation. The animation below illustrates this using a 16-bar blues bassline from Booker T. and MG’s classic Green Onions:
Reflection is also found in music composition, though it is far less common. It can be seen and heard in the first few bars of Beyoncé’s take on Ave Maria:

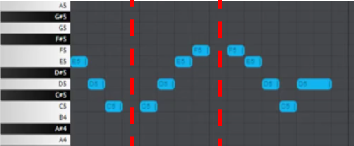
Dance
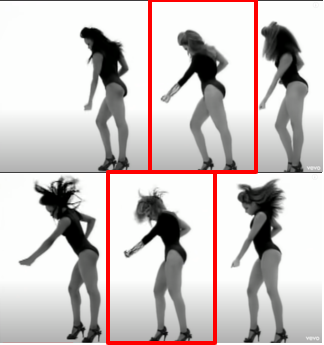
Dancers are also doing the mathematics of transformation. This can be seen clearly in Beyoncé’s Single Ladies video. In the first still from the video, the dancers maintain relative shape as they move through time and space — in other words, they are translating.
Transformations can also be seen as a form of symmetry within the arrangement of the dancers as in the images at below. And, of course, dancing involves multiple type of rotations that cannot be easily captured in a still image.

Reflection Symmetry 
Translation Symmetry

Hair
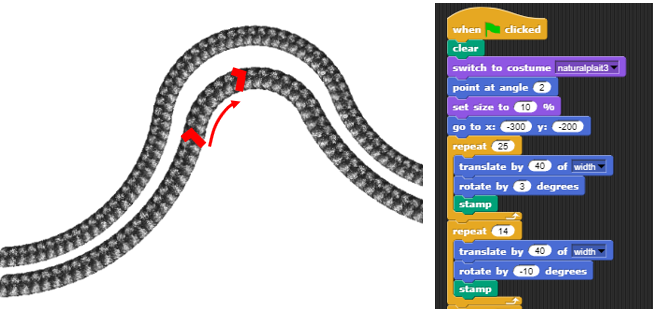
The designs commonly found in braids are cornrows are also forms of geometric transformation. Rotations, reflection, and translations can be found by looking at the larger design or by following the movement of individual plaits within a braid. The overall arch shape seen in Beyoncé’s hairstyle in the image has clear reflection symmetry. By zooming in, however, you can see each individual braid rotating slightly from one plait to the next.
Cornrows and braids are an intricate and complex mathematics. CSTD.org (Culturally Situated Design Tools) has a wealth of resources and tools to explore this mathematics in more depth. The image below shows a model of part of Beyoncé’s braid that was generated using CSTD’s coding tools.
What Counts?
I think its important to note that these examples must be shared with intentionality. In class, I think a great deal about how to avoid presenting these examples in what amounts to a cheesy appropriation of artistic ability and effort to sell math. I’m not sure I’m always successful, but my goal is to frame each with a deep appreciation of a complex and difficult skill that should be considered in and of itself to be math
In each of these examples, I do not believe that the math is only present at the moment of analysis. The singer flawlessly shifting keys, the jazz musician quickly transposing a song in their head, the dancer moving their body in line with others, the stylist gathering and braiding hair to follow a perfect curve are all doing math, just as much as the student plotting a triangle and reflecting it across the x-axis. The tools and expressions of the math may be different, but they are each navigating shape and space and wrestling with tension between disorder and order.
In a way, the arrows and diagrams I have added to illustrate the connections to school math degrade the complexity of the math performed in the above examples. It is not easy to sing a melody and then sing it again a half-step higher. I do not believe the examples above should exist just as context for “application” problems used in service of demonstrating school math. Rather, we should work for such expressions to be seen as math themselves.
Our students should see a math that is bigger than abstract representations, plotted points, and written notations. They should see a math that is active and participatory, that can use the mind and the body. It starts by help them, and us, question what counts as math.